三维张量轴变换(numpy的transpose方法)

最近在预习数据挖掘算法，学习numpy时，接触到一个概念，叫三维张量，在查阅资料和自己思考后，我终于搞明白这个东西了。但是我觉得网上的关于三维张量的资料比较少，而且大多都是介绍三维张量是什么，关于三维张量的轴变换的过程基本上都是略过，所以我写下了这篇文章来介绍三维张量的轴变换，也是对我思考成果的一个巩固。

大学学过的线性代数中的矩阵一般都是二维的，比如这样一个三阶矩阵:
(1 2 3
4 5 6
7 8 9),
从几何学的角度来看，我认为它是一个二维平面空间，

那么如何表示多维矩阵(张量)?比如三维矩阵，我们看一下下面这张图:

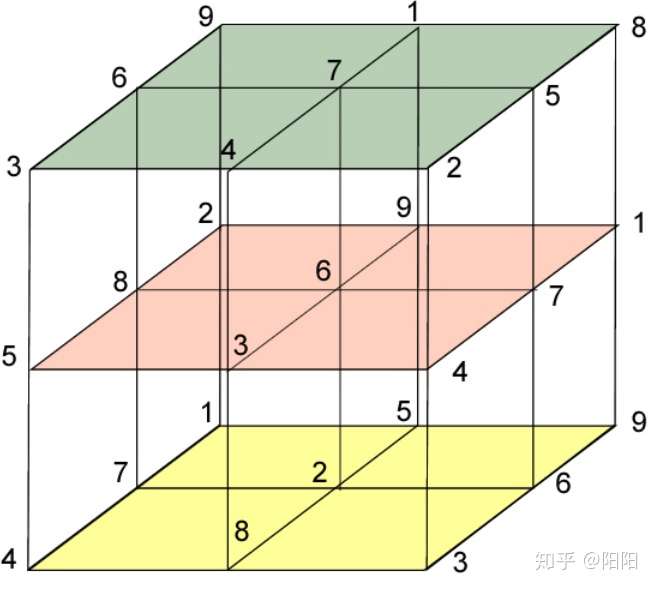
从这张图中，可以看出这个正方体的每一个”横向切面“都是一个二维矩阵，这些”横向切面“堆叠在一起就构成了”三维矩阵“，也就是三维张量。

这个三维张量在numpy中用ndarray对象来表示就是：

[[[9 1 8]
[6 7 5]
[3 4 2]]

[[2 9 1]
[8 6 7]
[5 3 4]]

[[1 5 9]
[7 2 6]
[4 8 3]]]

那么重点来了，我们如何进行三维张量的轴变换？以上面这个[3, 3, 3]三维张量为例，定义0为x轴，1为y轴，2为z轴

对0轴和1轴进行变换：

我们可以想象成是关于2轴方向对正方体进行”切片“，那么切下来的这些片分别是：

(9 1 8
2 9 1
1 5 9)

(6 7 5
8 6 7
7 2 6)

(3 4 2
5 3 4
4 8 3),

再把这些片按顺序自上往下堆叠起来，就完成了0轴和1轴的变换。其他情况下的轴变换以此类比。

参考资料：

numpy中的transpose函数使用方法

什么是张量

tensorflow2.0张量的维度变换