斐波那契递归详解

什么是斐波那契数列？

在数学上，斐波那契数列是这样定义的:

F₀ = 0

F₁ = 1

F_n = F_n-1 + F_n-2(n>=2)

假设n=3,那么F₃=F₂+F₁,此时F₁是已知的，且值为1,F₂未知。

下一步我们继续套用公式算F2，F₂=F₁+F₀，此时F₁和F₀都是已知的，且值都为0。就可以算出F₂=1+0=1。

有了F2，我们就可以算出F₃=1+1=2。

我们可以很轻易地推出n=1乃至n>=2的任意一个数:

1,1,2,3,5,8,13,21,34,55,89,…

如果想更多了解斐波那契数列，可以参考维基百科（需科学上网），不推荐使用百度百科（懂得都懂）

斐波那契数列的二叉树表示形式

话不多说，先放图:

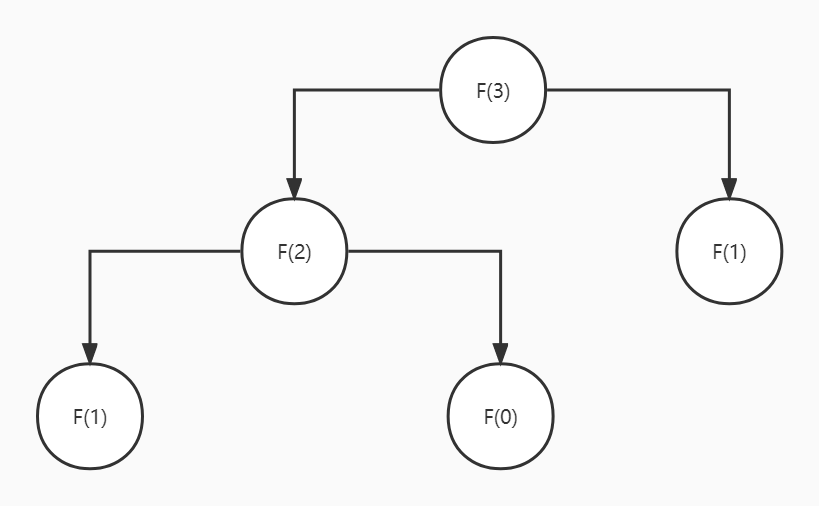
这是n=3时斐波那契数列的二叉树表示形式，观察一下可以看出叶子节点全部都是已知的值（可以理解为递归出口，意思就是“递归迷宫”走到这里就能出去了）。这个递归树怎么理解？实际上有点像动态规划，F₃是原问题的规模，把它分解为F₂和F₁两个规模更小的子问题，再把F₂分解为F₁和F₀。F₁可以分解吗？公式的条件给出了答案，n>=2时才可以分解，n=1和n=0时，已经是最小规模的了。

我们再来分析一下这个东西的结点数，我们来算一下这个树的结点有多少，2²+1，那么当规模趋向于n时，结点数就是2ⁿ指数级别。

剖析递归程序在计算机中的运行过程

我们先来看一下斐波那契数列递归实现的java代码:

int fibonacci(int n) {
		if(n == 0)
			return 0;
		if(n == 1)
			return 1;
		return fibonacci(n-1)+fibonacci(n-2);
}

其实这个过程用上面的二叉树表示图可以很清晰的解释，程序在算这个树的时候在中序遍历这个树，返回值的时候从叶节点开始返回，一直到整棵树的根节点。